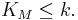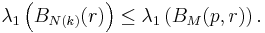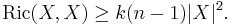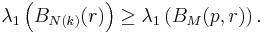Cheng's eigenvalue comparison theorem

In Riemannian geometry, Cheng's eigenvalue comparison theorem states in general terms that when a domain is large, the first Dirichlet eigenvalue of its Laplace–Beltrami operator is small. This general characterization is not precise, in part because the notion of "size" of the domain must also account for its curvature.^[1] The theorem is due to Cheng (1975b). Using geodesic balls, it can be generalized to certain tubular domains (Lee 1990).

Theorem

Let M be a Riemannian manifold with dimension n, and let B_M(p, r) be a geodesic ball centered at p with radius r less than the injectivity radius of p ∈ M. For each real number k, let N(k) denote the simply connected space form of dimension n and constant sectional curvature k. Cheng's eigenvalue comparison theorem compares the first eigenvalue λ₁(B_M(p, r)) of the Dirichlet problem in B_M(p, r) with the first eigenvalue in B_N(k)(r) for suitable values of k. There are two parts to the theorem:

• Suppose that K_M, the sectional curvature of M, satisfies

Then

The second part is a comparison theorem for the Ricci curvature of M:

• Suppose that the Ricci curvature of M satisfies, for every vector field X,

Then, with the same notation as above,

S.Y. Cheng used Barta's theorem to derive the eigenvalue comparison theorem. As a special case, if k = −1 and inj(p) = ∞, Cheng’s inequality becomes λ^*(N) ≥ λ^*(H ⁿ(−1)) which is McKean’s inequality.^[2]

See also

• Comparison theorem
• Eigenvalue comparison theorem

Notes

References

• Bessa, G.P.; Montenegro, J.F. (2008), "On Cheng's eigenvalue comparison theorem", Mathematical proceedings of the Cambridge Philosophical Society 144 (3): 673–682, ISSN 0305-0041 .
• Chavel, Isaac (1984), Eigenvalues in Riemannian geometry, Pure Appl. Math., 115, Academic Press .
• Cheng, Shiu Yuen (1975a), "Eigenfunctions and eigenvalues of Laplacian", Differential geometry (Proc. Sympos. Pure Math., Vol. XXVII, Stanford Univ., Stanford, Calif., 1973), Part 2, Providence, R.I.: American Mathematical Society, pp. 185–193, MR0378003 
• Cheng, Shiu Yuen (1975b), "Eigenvalue Comparison Theorems and its Geometric Applications", Math. Z. 143: 289–297, doi:10.1007/BF01214381 .
• Lee, Jeffrey M. (1990), "Eigenvalue Comparison for Tubular Domains", Proceedings of the American Mathematical Society (American Mathematical Society) 109 (3): 843–848, doi:10.2307/2048228, JSTOR 2048228 .
• McKean, Henry (1970), "An upper bound for the spectrum of △ on a manifold of negative curvature", J. Differ. Geom. 4: 359–366 .
• Lee, Jeffrey M.; Richardson, Ken (1998), "Riemannian foliations and eigenvalue comparison", Ann. Global Anal. Geom. 16: 497–525, doi:10.1023/A:1006573301591 /